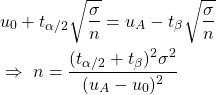Calculate Sample Size for A/B Testing hand by Hand Example

How to calculate the sample size in A/B testing that is necessary to achieve a hypothesis test with a certain power? We need to start by finding a threshold value c, such that if the sample mean is larger than c , we’ll reject the null hypothesis u₀.

$c = u_0 + t_{\alpha/2}\sqrt{\frac{\sigma}{n}}$

But, that’s not the only condition that c must meet, because c also needs to be defined to ensure that our power is 0.90 or, alternatively, that the probability of a Type II error is 0.10. That would happen if there was a 10% chance that our test statistic fail to reach c.

With alternative hypothesis u_A, we have:

$c = u_A - t_{\beta}\sqrt{\frac{\sigma}{n}}$

Now what we need to do is to equate the equation and solve for sample size n.

$\begin{align*} &u_0 + t_{\alpha/2}\sqrt{\frac{\sigma}{n}} = u_A - t_{\beta}\sqrt{\frac{\sigma}{n}} \\ &\Rightarrow \ n = \frac{(t_{\alpha/2}+t_\beta)^2\sigma^2}{(u_A-u_0)^2} \end{align*}$