Explain P-value in Layman's Terms

A p-value is probability that the data would be at least as extreme as those observed.

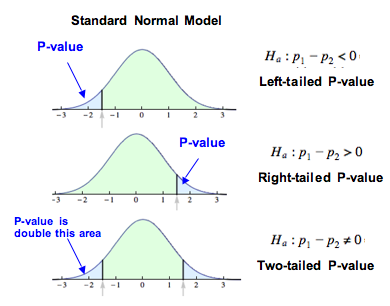
Is p-value a probability?

Yes and no. It’s the sum of the followings:

Probability of data that is rarer as those observed.
Probability of data that is equal to those observed.

Let’s look at an example of how to calculate p-value step-by-step.

Suppose you flipped a coin four times, and you want to find the p-value of observing three heads and one tail (noted as HHHT, ignoring the order).

$\begin{align*} P(HHHH) &= \frac{1}{16} \\ P(HHHT) &= \frac{1}{4} \\ P(HHTT) &=\frac{3}{8} \\ P(HTTT) &= \frac{1}{4} \\ P(TTTT) &= \frac{1}{16} \\ \end{align*}$

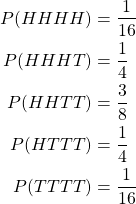
The probability of observing HHHT is

$P(HHHT) = \binom{3}{4} (\frac{1}{2})^4 = \frac{1}{4}$

The p-value of HHHT is different from the probability, in order to calculate it, first of all, we need to get:

Probability of data that is less likely to be observed compare to HHHT: P(HHHH) and P(TTTT)
Probability of data that is equally likely to be observed compare to HHHT: P(HTTT)

Summing them together we’ll get the p-value for HHHT:

$\begin{align*} \text{P-Value}(HHHT) &= P(HHHT) + P(HTTT) + P(HHHH) + P(TTTT) \\ &= \frac{1}{4} + \frac{1}{4} + \frac{1}{16} + \frac{1}{16} \\ &= \frac{5}{8} \end{align*}$

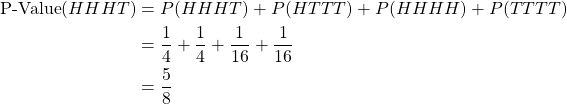
So the p-value of observing HHHT is: ⁵/₈. It is different from the probability of observing HHHT.